Understanding the mechanisms governing heat transfer in tubular systems is essential for the design and optimization of heat exchangers and similar equipment. This article provides a comparative analysis of several widely used correlations for calculating the heat transfer coefficient for fluid flow within tubes, detailing their theoretical basis, applicability, and limitations.

The heat transfer coefficient is a fundamental parameter in thermal engineering, representing the heat transfer rate per unit area per unit temperature difference between the fluid and the tube wall. Accurate estimation of this coefficient is crucial for efficient heat exchanger design, affecting everything from operational efficiency to equipment size and cost.

Heat transfer in tubes can occur via conduction, convection, and radiation, with convection being predominant in fluid flows. The convective heat transfer coefficient (h) depends on the properties of the fluid, the flow regime, and the tube's physical characteristics. It is typically calculated using dimensionless numbers like the Nusselt number (Nu), Reynolds number (Re), and Prandtl number (Pr).
For turbulent flow (Re > 10,000 and 0.7 < Pr < 160), the Dittus-Boelter equation is a popular choice:

This correlation is favored for its simplicity and reasonable accuracy in situations where the fluid properties do not vary significantly with temperature.
Modified to account for viscosity variations along the tube length, the Sieder-Tate correlation is more accurate for fluids with high viscosity or those whose viscosity changes with temperature:

where μ_b and μ_w are the fluid viscosities at the bulk fluid and wall temperatures, respectively.
Applicable for 0.5 < Pr < 2000 and 2300 < Re < 5 x 10^6, Gnielinski's correlation is derived from a wide range of experimental data and is expressed as:
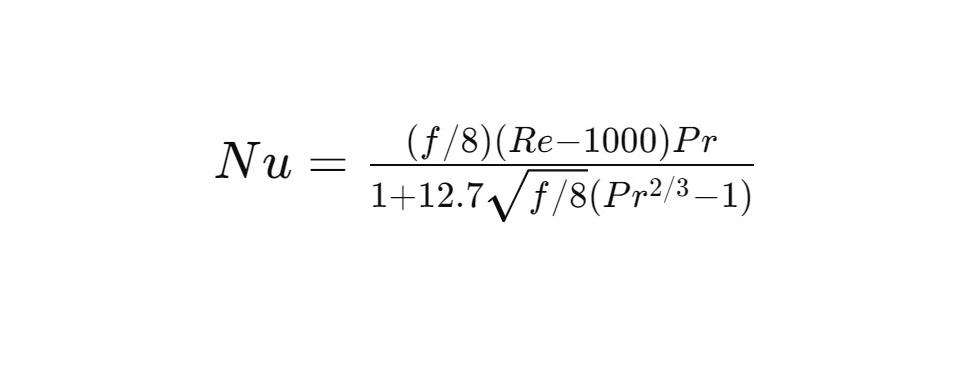
where f is the friction factor, which can be calculated using the Colebrook-White equation for smooth or rough tubes.
Selecting an appropriate correlation for calculating the heat transfer coefficient in tube flows requires consideration of the flow regime, fluid properties, and accuracy requirements. Engineers must balance the simplicity of application with the need for precision, depending on the specific operational conditions and design criteria.
This article has discussed several popular correlations, providing insights into their derivation, usage, and limitations, thus aiding in the informed selection and application of these correlations in various thermal system designs.